Recent searches
Search options
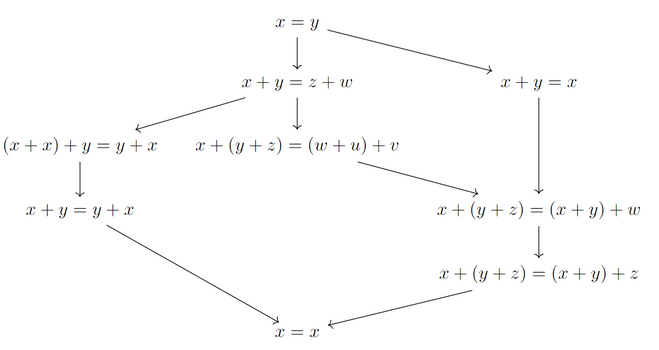
After posting an answer on this MathOverflow question https://mathoverflow.net/questions/450930/is-there-an-identity-between-the-associative-identity-and-the-constant-identity , I wonder if it might be a suitable graduate research project to see if current generation #ProofAssistant / #MachineLearning / #AI tools can be used to determine the logical relationship between various universal equational laws that could be satisfied by a single binary operation + on a set (i.e., by a magma). For instance, in the answer to this related question https://mathoverflow.net/questions/450890/is-there-an-identity-between-the-commutative-identity-and-the-constant-identity?noredirect=1&lq=1 it was shown (by a slightly intricate argument) that the law (𝑥+𝑥)+𝑦=𝑦+𝑥 implies the commutative law 𝑥+𝑦=𝑦+𝑥, but not conversely, while I showed that the law 𝑥+(𝑦+𝑧)=(𝑥+𝑦)+𝑤 is strictly intermediate between the triple constant law 𝑥+(𝑦+𝑧)=(𝑤+𝑢)+𝑣 and the associative law 𝑥+(𝑦+𝑧)=(𝑥+𝑦)+𝑧. It seems that this is a restrictive enough fragment of #mathematics (or even of #UniversalAlgebra) that automated tools should function rather well, without being so trivial as to be completely solvable by brute force.
@tao The universal algebra community has had tools for this for sort of thing for a long time. For instance, you can check out https://www.cs.unm.edu/~mccune/prover9/. It would be interesting to see more continuous methods like neural nets combined with tools like these to impart some more human intuition. I was actually asking @ProfKinyon about this earlier this month.
@caten @tao Yeah, once candidate identities are given, any automated theorem prover can handle the task of sorting out how different varieties (in the universal algebra sense, i.e., equational classes) are contained in other varieties. Generating the candidate identities (subject to reasonable constraints) would be the other part of it.
@ProfKinyon @caten There is a third task here which could potentially benefit from AI tools: trying to *disprove* an implication of one identity from another by producing a magma which obeys the former identity but not the latter. One could imagine using machine learning to generate candidate magmas that are likely to achieve this goal, and then using an SMT solver or something to formally verify.
A fourth task that is rather vague, but perhaps closest to replicating human intuition, is to develop some way of automatically assessing whether a given identity (or conjunction of identities) is "strong" or "weak", either in absolute terms or relative to some other collection of identities, allowing one to possibly strategize proofs or disproofs of implications by splitting the task into smaller pieces, as I discussed in a recent post.
@ProfKinyon @caten Perhaps I can pose a concrete challenge to focus the discussion. Consider the collection of all possible universal equational laws in which the magma operation + is applied at most four times. For instance, the associative law (𝑥+𝑦)+𝑧=𝑥+(𝑦+𝑧)) is of this form. I don't know exactly how many such laws exist, up to relabeling and symmetries, but let's say for sake of argument that there are around a thousand. The (admittedly artificial) challenge is to completely specify the partial ordering on this collection given by implication, thus extending the diagram included here to the other thousand or so identities involving at most four operations. Is this feasible to accomplish by some combination of current automated tools and reasonable number of human expert-hours? Note that one has not only to prove those implications that happen to be true, but also to disprove those implications that happen to be false. One could blindly throw random implications into various automated theorem provers, but would it actually be computationally feasible to completely specify the million or so implications this way? Or would some sort of automated "intuition" coming perhaps from machine learning tools be a significant speedup?
@tao @ProfKinyon As far as the number of such equations goes, the number of bracketings of n variables is given by the Catalan numbers, so you could likely give the exact count of the number of formulas of a certain size in terms of those and any symmetry you want to quotient out by, assuming you were okay going by the number of variables appearing rather than the height (number of applications of the operations). Similar ideas should work for counting by height instead, I'd imagine.
Anyway, my initial guess is that this task has a chance of being undecidable in general. I don't have a proof, but some similar tasks are impossible. First, there are finite magmas that generate varieties which are not finitely based (i.e. there is no finite list of equations which imply all others that are true for the magma). Second, some varieties have an undecidable equational theory (i.e. there cannot exist an algorithm for checking whether a general equation is true in that variety). Third, the lattice of clones on a set with even three elements is already uncountable. While you would only have us look at a finite fragment of a countable part of this lattice (the varieties axiomatized by a single identity), I feel unsure that such an algorithm can exist.
This isn't to say that you couldn't typically make the decision, but I also wouldn't bank on it being effectively solvable for all relatively small equations.
@caten @ProfKinyon It looks a bit more complicated to me than Catalan numbers due to the ability to repeat variables, but certainly I could imagine a brute force search could enumerate these formulae reasonably quickly. (I am somewhat tempted to try out GPT-4's vaunted code generation ability for this task, though I foresee that debugging such AI-generated code could be more time-consuming than writing the code by more traditional means.)
I agree that likely there will be undecidable implications at some point. But perhaps a reasonable goal is to have automation work out the truth or falsity of, say, 90% of all possible implications, and then of the remaining 10%, isolate the most "interesting" or "critical" 1% to then pose to human experts. Perhaps humans can resolve all but 0.1% of these critical implications, which one can then pose as open conjectures. [These percentages are completely made up, of course.]
I also have the hope that even just having 90% of the implication graph might reveal some interesting features that would not have been obvious to human experts who might only encounter O(1) of these equational laws at a time, and were previously not able to explore the more global structure of the space of laws. (For instance, is there a phenomenon similar to that in reverse mathematics where many arithmetic theories seem to collapse to one of the "big five"?)
@tao @ProfKinyon I was originally going to say that I wouldn't be surprised if this was the case, but the more I think about it the less sure I am. It's true that while universal algebra has at this point considerable tools for handling arbitrary varieties of algebras, most of the ones people actually study are either "like groups" or "like lattices". One idea is that the ones that are too alien are too degenerate, but it could also be that studying them is too hard, even with computer help, so we will always be stuck in the small tractable region we have already found.
It is true that a randomly-chosen finite algebra will be primal with probability 1 (Murskiĭ's Theorem), so most finite algebras can be thought of as basically identical from an equational perspective, up to relabeling the basic operations. However, the number of algebras grows very quickly up to isomorphism, so checking whether a given algebra is "trivial" in this sense may rarely be attainable. See https://www.ams.org/journals/proc/1966-017-03/S0002-9939-1966-0200219-9/S0002-9939-1966-0200219-9.pdf.