Recent searches
Search options
From 2013 to 2017 I ran a blog called Visual Insight, which was a place to share striking images that help explain topics in mathematics. Last week I gave a talk about it at the Illustrating Math Seminar. Now you can see the video here:
https://www.youtube.com/watch?v=6G611RbO3GQ
It was fun explaining some great images created by @RefurioAnachro, @gregeganSF, @roice3, @GerardWestendorp and other folks. For more info on the images I talked about, go here:
• http://math.ucr.edu/home/baez/visual_insight/20150115%20-%20Hammersley%20Sofa.html 2015 - 01 - 15 — Hammersley Sofa
• http://math.ucr.edu/home/baez/visual_insight/20151201%20-%20Golay%20Code.html 2015 - 12 - 01 — Golay Code
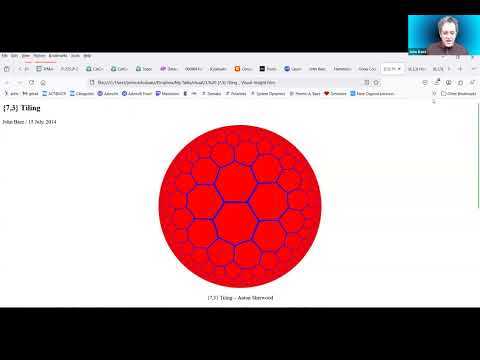
• http://math.ucr.edu/home/baez/visual_insight/20140715%20-%20%7b7,3%7d%20Tiling.html 2014 - 07 - 15 — {7,3} Tiling
• http://math.ucr.edu/home/baez/visual_insight/20140315%20-%20%7b6,3,3%7d%20Honeycomb.html 2014 - 03 - 15 — {6,3,3} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20130915%20-%20%7b6,3,3%7d%20Honeycomb%20in%20Upper%20Half%20Space.html 2013 - 09 - 15 — {6,3,3} Honeycomb in Upper Half Space
• http://math.ucr.edu/home/baez/visual_insight/20151215%20-%20Kaleidocycle.html 2015 - 12 - 15 — Kaleidocycle
• http://math.ucr.edu/home/baez/visual_insight/20160215%20-%2027%20Lines%20on%20a%20Cubic%20Surface.html 2016 - 02 - 15 — 27 Lines on a Cubic Surface
• http://math.ucr.edu/home/baez/visual_insight/20150415%20-%20Sphere%20in%20Mirrored%20Spheroid.html 2015 - 04 - 15 — Sphere in Mirrored Spheroid
• http://math.ucr.edu/home/baez/visual_insight/20151001%20-%20Balaban%2010-Cage.html 2015 - 10 - 01 — Balaban 10-Cage
• http://math.ucr.edu/home/baez/visual_insight/20150915%20-%20McGee%20Graph.html 2015 - 09 - 15 — McGee Graph
You can see the whole blog at the AMS website:
https://blogs.ams.org/visualinsight/author/johnbaez/AMS website
or on my own website in a more stripped-down format:
https://math.ucr.edu/home/baez/visual_insight/my website. But you can also check out individual articles here.... (Yes, read on....)
(1/n)
Here are the articles from 2013. Which one am I featuring here?
• http://math.ucr.edu/home/baez/visual_insight/20130815%20-%20T%fcbingen%20Tiling.html 2013 - 08 - 15 — Tübingen Tiling
• http://math.ucr.edu/home/baez/visual_insight/20130901%20-%20Algebraic%20Numbers.html 2013 - 09 - 01 — Algebraic Numbers
• http://math.ucr.edu/home/baez/visual_insight/20130915%20-%20%7b6,3,3%7d%20Honeycomb%20in%20Upper%20Half%20Space.html 2013 - 09 - 15 — {6,3,3} Honeycomb in Upper Half Space
• http://math.ucr.edu/home/baez/visual_insight/20131001%20-%20Catacaustic%20of%20a%20Cardioid.html 2013 - 10 - 01 — Catacaustic of a Cardioid
• http://math.ucr.edu/home/baez/visual_insight/20131015%20-%20Atomic%20Singular%20Inner%20Function.html 2013 - 10 - 15 — Atomic Singular Inner Function
• http://math.ucr.edu/home/baez/visual_insight/20131101%20-%20Enneper%20Surface.html 2013 - 11 - 01 — Enneper Surface
• http://math.ucr.edu/home/baez/visual_insight/20131115%20-%20Astroid%20as%20Catacaustic%20of%20Deltoid.html 2013 - 11 - 15 — Astroid as Catacaustic of Deltoid
• http://math.ucr.edu/home/baez/visual_insight/20131201%20-%20Deltoid%20Rolling%20Inside%20Astroid.html 2013 - 12 - 01 — Deltoid Rolling Inside Astroid
• http://math.ucr.edu/home/baez/visual_insight/20131215%20-%20Truncated%20Hypercube.html 2013 - 12 - 15 — Truncated Hypercube
(2/n)
Here are the pictures from 2014:
• http://math.ucr.edu/home/baez/visual_insight/20140101%20-%20Pentagon-Hexagon-Decagon%20Identity.html 2014 - 01 - 01 — Pentagon-Hexagon-Decagon Identity
• http://math.ucr.edu/home/baez/visual_insight/20140115%20-%20Weierstrass%20Elliptic%20Function.html 2014 - 01 - 15 — Weierstrass Elliptic Function
• http://math.ucr.edu/home/baez/visual_insight/20140201%20-%20%7b5,3,5%7d%20Honeycomb.html 2014 - 02 - 01 — {5,3,5} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20140215%20-%20Cantor%92s%20Cube.html 2014 - 02 - 15 — Cantor’s Cube
• http://math.ucr.edu/home/baez/visual_insight/20140301%20-%20Menger%20Sponge.html 2014 - 03 - 01 — Menger Sponge
• http://math.ucr.edu/home/baez/visual_insight/20140315%20-%20%7b6,3,3%7d%20Honeycomb.html 2014 - 03 - 15 — {6,3,3} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20140401%20-%20%7b6,3,4%7d%20Honeycomb.html 2014 - 04 - 01 — {6,3,4} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20140415%20-%20%7b6,3,5%7d%20Honeycomb.html 2014 - 04 - 15 — {6,3,5} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20140515%20-%20Pattern-Equivariant%20Homology%20of%20a%20Penrose%20Tiling.html 2014 - 05 - 15 — Pattern-Equivariant Homology of a Penrose Tiling
• http://math.ucr.edu/home/baez/visual_insight/20140601%20-%20Grace-Danielsson%20Inequality.html 2014 - 06 - 01 — Grace–Danielsson Inequality
• http://math.ucr.edu/home/baez/visual_insight/20140615%20-%20Origami%20Dodecahedra.html 2014 - 06 - 15 — Origami Dodecahedra
• http://math.ucr.edu/home/baez/visual_insight/20140701%20-%20Sierpinski%20Carpet.html 2014 - 07 - 01 — Sierpinski Carpet
• http://math.ucr.edu/home/baez/visual_insight/20140715%20-%20%7b7,3%7d%20Tiling.html 2014 - 07 - 15 — {7,3} Tiling
• http://math.ucr.edu/home/baez/visual_insight/20140801%20-%20%7b7,3,3%7d%20Honeycomb.html 2014 - 08 - 01 — {7,3,3} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20140814%20-%20%7b7,3,3%7d%20Honeycomb%20Meets%20Plane%20at%20Infinity.html 2014 - 08 - 15 — {7,3,3} Honeycomb Meets Plane at Infinity
• http://math.ucr.edu/home/baez/visual_insight/20140901%20-%20%7b3,3,7%7d%20Honeycomb%20Meets%20Plane%20at%20Infinity.html 2014 - 09 - 01 — {3,3,7} Honeycomb Meets Plane at Infinity
• http://math.ucr.edu/home/baez/visual_insight/20140915%20-%20Pr%fcfer%202-Group.html 2014 - 09 - 15 — Prüfer 2-Group
• http://math.ucr.edu/home/baez/visual_insight/20141001%20-%202-adic%20Integers.html 2014 - 10 - 01 — 2-adic Integers
• http://math.ucr.edu/home/baez/visual_insight/20141015%20-%20Packing%20Regular%20Octagons.html 2014 - 10 - 15 — Packing Regular Octagons
• http://math.ucr.edu/home/baez/visual_insight/20141101%20-%20Packing%20Smoothed%20Octagons.html 2014 - 11 - 01 — Packing Smoothed Octagons
• http://math.ucr.edu/home/baez/visual_insight/20141115%20-%20Packing%20Regular%20Heptagons.html 2014 - 11 - 15 — Packing Regular Heptagons
• http://math.ucr.edu/home/baez/visual_insight/20141201%20-%20Packing%20Regular%20Pentagons.html 2014 - 12 - 01 — Packing Regular Pentagons
(3/n)
Here are the pictures from 2015:
• http://math.ucr.edu/home/baez/visual_insight/20150101%20-%20Icosidodecahedron%20from%20D6.html 2015 - 01 - 01 — Icosidodecahedron from D6
• http://math.ucr.edu/home/baez/visual_insight/20150115%20-%20Hammersley%20Sofa.html 2015 - 01 - 15 — Hammersley Sofa
• http://math.ucr.edu/home/baez/visual_insight/20150201%20-%20Pentagon-Decagon%20Packing.html 2015 - 02 - 01 — Pentagon-Decagon Packing
• http://math.ucr.edu/home/baez/visual_insight/20150215%20-%20Pentagon-Decagon%20Branched%20Covering.html 2015 - 02 - 15 — Pentagon-Decagon Branched Covering
• http://math.ucr.edu/home/baez/visual_insight/20150301%20-%20Schmidt%20Arrangement.html 2015 - 03 - 01 — Schmidt Arrangement
• http://math.ucr.edu/home/baez/visual_insight/20150315%20-%20Small%20Cubicuboctahedron.html 2015 - 03 - 15 — Small Cubicuboctahedron
• http://math.ucr.edu/home/baez/visual_insight/20150401%20-%20Branched%20Cover%20from%20(4%204%203_2)%20Schwarz%20Triangle.html 2015 - 04 - 01 — Branched Cover from (4 4 3/2) Schwarz Triangle
• http://math.ucr.edu/home/baez/visual_insight/20150415%20-%20Sphere%20in%20Mirrored%20Spheroid.html 2015 - 04 - 15 — Sphere in Mirrored Spheroid
• http://math.ucr.edu/home/baez/visual_insight/20150501%20-%20Twin%20Dodecahedra.html 2015 - 05 - 01 — Twin Dodecahedra
• http://math.ucr.edu/home/baez/visual_insight/20150515%20-%20Dodecahedron%20With%205%20Tetrahedra.html 2015 - 05 - 15 — Dodecahedron With 5 Tetrahedra
• http://math.ucr.edu/home/baez/visual_insight/20150601%20-%20Harmonic%20Orbit.html 2015 - 06 - 01 — Harmonic Orbit
• http://math.ucr.edu/home/baez/visual_insight/20150615%20-%20Lattice%20of%20Partitions.html 2015 - 06 - 15 — Lattice of Partitions
• http://math.ucr.edu/home/baez/visual_insight/20150701%20-%20Petersen%20Graph.html 2015 - 07 - 01 — Petersen Graph
• http://math.ucr.edu/home/baez/visual_insight/20150715%20-%20Dyck%20Words.html 2015 - 07 - 15 — Dyck Words
• http://math.ucr.edu/home/baez/visual_insight/20150801%20-%20Heawood%20Graph.html 2015 - 08 - 01 — Heawood Graph
• http://math.ucr.edu/home/baez/visual_insight/20150815%20-%20Tutte-Coxeter%20Graph.html 2015 - 08 - 15 — Tutte–Coxeter Graph
• http://math.ucr.edu/home/baez/visual_insight/20150901%20-%20Hypercube%20of%20Duads.html 2015 - 09 - 01 — Hypercube of Duads
• http://math.ucr.edu/home/baez/visual_insight/20150915%20-%20McGee%20Graph.html 2015 - 09 - 15 — McGee Graph
• http://math.ucr.edu/home/baez/visual_insight/20151001%20-%20Balaban%2010-Cage.html 2015 - 10 - 01 — Balaban 10-Cage
• http://math.ucr.edu/home/baez/visual_insight/20151015%20-%20Harries%20Graph.html 2015 - 10 - 15 — Harries Graph
• http://math.ucr.edu/home/baez/visual_insight/20151101%20-%20Balaban%2011-Cage.html 2015 - 11 - 01 — Balaban 11-Cage
• http://math.ucr.edu/home/baez/visual_insight/20151115%20-%20Newton%92s%20Apsidal%20Precession%20Theorem.html 2015 - 11 - 15 — Newton’s Apsidal Precession Theorem
• http://math.ucr.edu/home/baez/visual_insight/20151201%20-%20Golay%20Code.html 2015 - 12 - 01 — Golay Code
• http://math.ucr.edu/home/baez/visual_insight/20151215%20-%20Kaleidocycle.html 2015 - 12 - 15 — Kaleidocycle
Here are the pictures from 2016, and one from 2017.
• http://math.ucr.edu/home/baez/visual_insight/20160101%20-%20Free%20Modular%20Lattice%20on%203%20Generators.html 2016 - 01 - 01 — Free Modular Lattice on 3 Generators
• http://math.ucr.edu/home/baez/visual_insight/20160115%20-%20Cairo%20Tiling.html 2016 - 01 - 15 — Cairo Tiling
• http://math.ucr.edu/home/baez/visual_insight/20160201%20-%20Hoffman-Singleton%20Graph.html 2016 - 02 - 01 — Hoffman–Singleton Graph
• http://math.ucr.edu/home/baez/visual_insight/20160215%20-%2027%20Lines%20on%20a%20Cubic%20Surface.html 2016 - 02 - 15 — 27 Lines on a Cubic Surface
• http://math.ucr.edu/home/baez/visual_insight/20160301%20-%20Clebsch%20Surface.html 2016 - 03 - 01 — Clebsch Surface
• http://math.ucr.edu/home/baez/visual_insight/20160315%20-%20Zamolodchikov%20Tetrahedron%20Equation.html 2016 - 03 - 15 — Zamolodchikov Tetrahedron Equation
• http://math.ucr.edu/home/baez/visual_insight/20160401%20-%20Rectified%20Truncated%20Icosahedron.html 2016 - 04 - 01 — Rectified Truncated Icosahedron
• http://math.ucr.edu/home/baez/visual_insight/20160415%20-%20Barth%20Sextic.html 2016 - 04 - 15 — Barth Sextic
• http://math.ucr.edu/home/baez/visual_insight/20160501%20-%20Involutes%20of%20a%20Cubical%20Parabola.html 2016 - 05 - 01 — Involutes of a Cubical Parabola
• http://math.ucr.edu/home/baez/visual_insight/20160515%20-%20Discriminant%20of%20the%20Icosahedral%20Group.html 2016 - 05 - 15 — Discriminant of the Icosahedral Group
• http://math.ucr.edu/home/baez/visual_insight/20160601%20-%20Discriminant%20of%20Restricted%20Quintic.html 2016 - 06 - 01 — Discriminant of Restricted Quintic
• http://math.ucr.edu/home/baez/visual_insight/20160615%20-%20Small%20Stellated%20Dodecahedron.html 2016 - 06 - 15 — Small Stellated Dodecahedron
• http://math.ucr.edu/home/baez/visual_insight/20160701%20-%20Barth%20Decic.html 2016 - 07 - 01 — Barth Decic
• http://math.ucr.edu/home/baez/visual_insight/20160715%20-%20Labs%20Septic.html 2016 - 07 - 15 — Labs Septic
• http://math.ucr.edu/home/baez/visual_insight/20160801%20-%20Endrass%20Octic.html 2016 - 08 - 01 — Endrass Octic
• http://math.ucr.edu/home/baez/visual_insight/20160815%20-%20Cayley%92s%20Nodal%20Cubic%20Surface.html 2016 - 08 - 15 — Cayley’s Nodal Cubic Surface
• http://math.ucr.edu/home/baez/visual_insight/20160901%20-%20Kummer%20Quartic.html 2016 - 09 - 01 — Kummer Quartic
• http://math.ucr.edu/home/baez/visual_insight/20160915%20-%20Togliatti%20Quintic.html 2016 - 09 - 15 — Togliatti Quintic
• http://math.ucr.edu/home/baez/visual_insight/20161001%20-%20Diamond%20Cubic.html 2016 - 10 - 01 — Diamond Cubic
• http://math.ucr.edu/home/baez/visual_insight/20161015%20-%20Laves%20Graph.html 2016 - 10 - 15 — Laves Graph
• http://math.ucr.edu/home/baez/visual_insight/20161101%20-%20Escudero%20Nonic.html 2016 - 11 - 01 — Escudero Nonic
• http://math.ucr.edu/home/baez/visual_insight/20161116%20-%20Bunimovich%20Stadium.html 2016 - 11 - 15 — Bunimovich Stadium
• http://math.ucr.edu/home/baez/visual_insight/20161201%20-%20Truncated%20%7b6,3,3%7d%20Honeycomb.html 2016 - 12 - 01 — Truncated {6,3,3} Honeycomb
• http://math.ucr.edu/home/baez/visual_insight/20161215%20-%20Romik%92s%20Ambidextrous%20Sofa.html 2016 - 12 - 15 — Romik’s Ambidextrous Sofa
• http://math.ucr.edu/home/baez/visual_insight/20170101%20-%20Chmutov%20Octic.html 2017 - 01 - 01 — Chmutov Octic
(5/n, n = 5)
Abdelaziz Nait Merzouk made gorgeous renderings! They are really something to aspire to. I would really like to make similar ones in shadertoy. First get a Newton root finder implemented and then see what I can do with that. Another inspiration is to try and get something like @KangarooPhysics's Seifert-like surfaces for knots.
Yet another project idea is to write a relativistic raymarcher, to render black holes and some other, more weird 4d stuff.
I'm kind of obliged to something along these lines, because I promised some guys to show off with them at the next Evoke demo party in Cologne. That means I have about half a year to get it done, which should be plenty. Should...