Recent searches
Search options
The number pi has an evil twin! It's a number called ϖ with many properties similar to π. There are even mutant trig functions connected to this number, called sl and cl.
So maybe while you were studying trig in high school, some kid in another galaxy was having to memorize all the identities for these other functions.
I doubt it. Just as pi and trig functions are connected to the circle, this number ϖ and its mutant trig functions are connected to a curve shaped like the symbol for infinity, ∞. But this curve is just less important than the circle. I'm not enough of a cultural relativist to believe there's a civilization that cares more about the shape ∞ than the shape ◯.
This ∞-shaped curve is called a 'lemniscate', and ϖ is called the 'lemniscate constant'. I'll show you the lemniscate in my next post.
A civilization will probably only get interested in ϖ when it gets interested in the lemniscate.... or the deeper math it's connected to. On our planet, it was Bernoulli, Euler and Gauss who discovered this math.
(Why does unicode even have the symbol ϖ? Here's why: it's a script version of the Greek letter pi, sometimes called 'varpi' or 'pomega'.)
(1/n)
![The lemniscate constant $\varpi$ is like a mutant version of the number $\pi$:
\[ \pi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^2}} \approx 3.14159 \]
\[ \varpi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^4}} \approx 2.622057 \]
It obeys a lot of similar formulas. For example:
\[ \frac2\pi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12\sqrt{\frac12 + \frac12\sqrt\frac12}} \cdots \]
\[
\frac2\varpi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12 \Bigg/ \!\sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12}} \cdots
\]](https://media.mathstodon.xyz/media_attachments/files/113/703/358/405/037/392/original/12262b712b868b80.jpg "The lemniscate constant $\varpi$ is like a mutant version of the number $\pi$:
\[ \pi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^2}} \approx 3.14159 \]
\[ \varpi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^4}} \approx 2.622057 \]
It obeys a lot of similar formulas. For example:
\[ \frac2\pi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12\sqrt{\frac12 + \frac12\sqrt\frac12}} \cdots \]
\[
\frac2\varpi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12 \Bigg/ \!\sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12}} \cdots
\]")
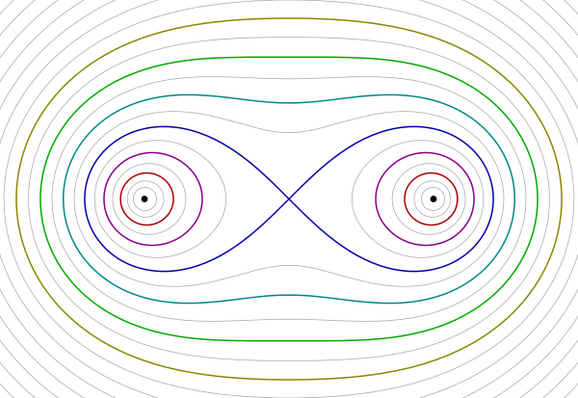
Take 2 points. Draw all the curves where the product of the distances from these 2 points is some constant or other. These are called the 'ovals of Cassini'.
There's one that's special, shaped like ∞. This is the 'lemniscate'. This is the one connected to pi's evil twin.
Here's a formula for the lemniscate in polar coordinates:
r² = cos2θ
Just as the perimeter of the unit circle is 2π, the perimeter of this curve is 2ϖ where
ϖ ≈ 2.62205755...
People have computed this number to over a trillion digits.
Just as we can use the circle to define the trig functions sin and cos, we can use this curve to define functions called sl and cl. Most of the usual trig identities have mutant versions that work for sl and cl. For example just as we have
sin²θ + cos²θ = 1
we have
sl²θ + cl²θ + sl²θ cl²θ = 1
To see a graph of sl and cl, go here:
https://en.wikipedia.org/wiki/Lemniscate_elliptic_functions
But I want to show you some formulas for π and ϖ!
(2/n)
@johncarlosbaez
I really don't understand this: "Just as the perimeter of a circle is 2π, the perimeter of this curve is 2ϖ".
Well, technically, the perimeter of a circle is 2π time its radius, so I expect the lemniscate's perimeter is 2ϖ times "some radius". What is it? On a circle it's obvious but not on an 8-shaped curve.
@gsrdzl - I should indeed have said the perimeter of the *unit* circle is 2π. I'll fix that. Thanks. The rest, I think, is clear:
"Here's a formula for the lemniscate in polar coordinates:
r² = cos2θ
Just as the perimeter of [the unit] circle is 2π, the perimeter of this curve is 2ϖ where
ϖ ≈ 2.62205755..."
So, "this curve" is the curve I wrote down above.
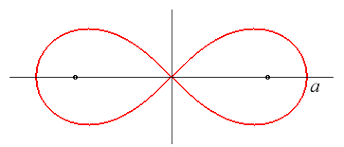
Here's another way to put it: the perimeter of the curve
𝑥²+𝑦²=1
is 2π, and the perimeter of the following version of Bernoulli's lemniscate is 2ϖ:
(𝑥²+𝑦²)² = 𝑥²−𝑦²
This is the same as I wrote down in polar coordinates above.
@johncarlosbaez
OK. According to Wikipedia, the equation for a Bernoulli's lemniscate in the general case is
(𝑥²+𝑦²)² = a²(𝑥²−𝑦²).
So, is the parameter a the analogue of a radius? In other words, is the perimeter of a non-unit lemniscate equal to 2ϖa?
@gsrdzl - yes, a is analogous to the radius. And I now see that a is the distance between the origin and the rightmost point on this lemniscate:
(𝑥²+𝑦²)² = a²(𝑥²−𝑦²).
since that point has x = a, y = 0. So it is geometrically not a terrible concept of radius!
Thanks for making Christmas more fun.
@johncarlosbaez Thanks to you. I've learned a lot.