Recent searches
Search options
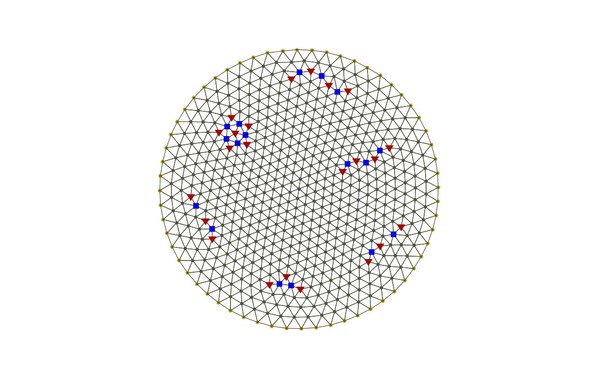
This shows a 2-dimensional 'electron crystal', formed when very cold electrons at low density are confined to a disk. The vertices are the electrons. The edges are just to help you see the pattern.
To minimize energy, the pattern wants to be a lattice of equilateral triangles. But since such a lattice doesn’t fit neatly into a disk, there are also some red and blue ‘defects'.
5 triangles meet at each red vertex. 7 meet at each blue vertex.
Now it's time to make some conjectures!
(1/n)
Take N points 𝑥ᵢ on the unit disk, arranged so as to minimize the energy
I conjecture that when N is large, when we form the Delauney triangulation of these points, most points will be connected to 6 others, while those on the boundary will be connected to 4. There will also be 'red and blue defects' - points connected to 5 or 7 others.
And I conjecture that there will be 6 more red defects than blue defects!
(2/n)
I don't have much evidence for this conjecture. But I have a hand-wavy argument for why there should be 6 more red defects than blue ones. It's here:
https://johncarlosbaez.wordpress.com/2017/12/07/wigner-crystals/
The easiest way forward would be to take N points on the unit disk, and use some algorithm to move them around until their energy is approximately minimized, and then work out the Delauney triangulation:
https://en.wikipedia.org/wiki/Delaunay_triangulation
and count the defects of various kinds. If you give it a try, let me know!
(3/n, n = 3)
@johncarlosbaez I just want to point to the reference https://arxiv.org/pdf/cond-mat/9707204.pdf (section V and Appendix A), where they discuss the same.
@The_Correlator - excellent, thanks! This topic is mainly a hobby for me so I haven't been digging into the literature. I'm glad to know that experts are thinking about this.