Recent searches
Search options
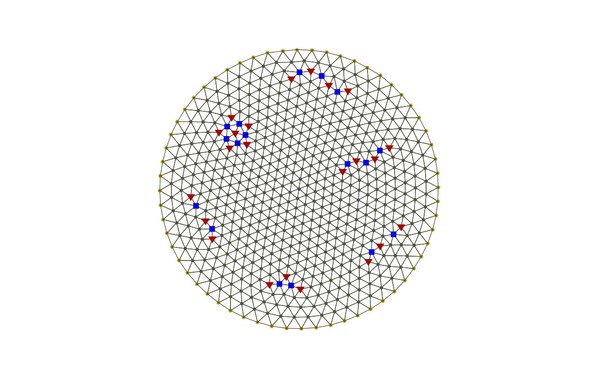
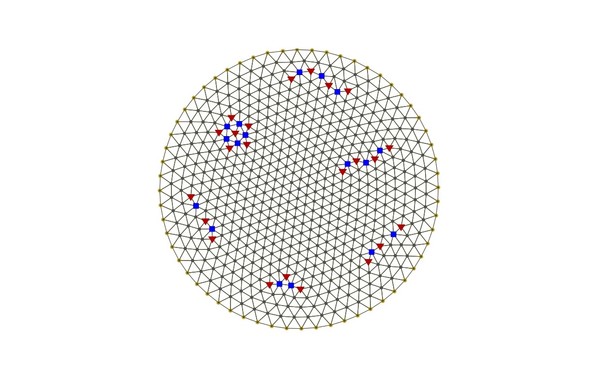
This shows a 2-dimensional 'electron crystal', formed when very cold electrons at low density are confined to a disk. The vertices are the electrons. The edges are just to help you see the pattern.
To minimize energy, the pattern wants to be a lattice of equilateral triangles. But since such a lattice doesn’t fit neatly into a disk, there are also some red and blue ‘defects'.
5 triangles meet at each red vertex. 7 meet at each blue vertex.
Now it's time to make some conjectures!
(1/n)
Take N points 𝑥ᵢ on the unit disk, arranged so as to minimize the energy
I conjecture that when N is large, when we form the Delauney triangulation of these points, most points will be connected to 6 others, while those on the boundary will be connected to 4. There will also be 'red and blue defects' - points connected to 5 or 7 others.
And I conjecture that there will be 6 more red defects than blue defects!
(2/n)
I don't have much evidence for this conjecture. But I have a hand-wavy argument for why there should be 6 more red defects than blue ones. It's here:
https://johncarlosbaez.wordpress.com/2017/12/07/wigner-crystals/
The easiest way forward would be to take N points on the unit disk, and use some algorithm to move them around until their energy is approximately minimized, and then work out the Delauney triangulation:
https://en.wikipedia.org/wiki/Delaunay_triangulation
and count the defects of various kinds. If you give it a try, let me know!
(3/n, n = 3)
@johncarlosbaez Maybe Euler's formula can be used here? A related well-known fact about e.g. 3D meshes (triangulations of closed surfaces) is that on average every vertex has degree 6 (the exact value is 6-\chi(X)/12V or something like that).
@lisyarus - yes, if you read my article about this you'll see I use Euler's formula to heuristically argue for 6 more red defects than blue ones:
https://johncarlosbaez.wordpress.com/2017/12/07/wigner-crystals/
But it's not a proof!
@johncarlosbaez Ah, I see!
Now I'm also incredibly tempted to write some simulation that would do the thing with any number of points...
@johncarlosbaez Interestingly, I consistently get results that look more like this, i.e. density gets higher closer to the disk edge
@johncarlosbaez Oh, I've read the wiki article and they say they have an extra parabolic potential added to the system. Gonna try that as well.
@lisyarus - Very nice result! Sorry, I forgot to mention the quadratic potential. If it's easy to run 100 simulations with different number of points and see if there are always 6 more red defects than blue ones, that would be cool.