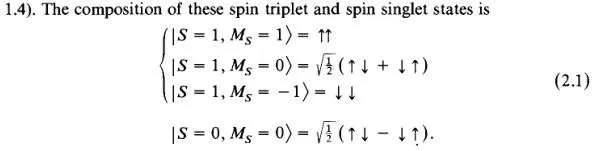Back

One of the basic things you learn in #quantum mechanics is that 2 spins can be in a state of definite total angular momentum J^2.

In elementary textbooks, this is usually presented as a spin singlet and triplet (see image). It seems simple, but how do you know that you understand what has been done and are not just reciting what you have seen? A good way to test your knowledge is to recreate the same approach for 3 spins which some researchers may struggle with.

It is true that you will have a total spin 3/2 state with 4 J_z eigenstates and a spin 1/2 state with 2 J_z eigenstates. But this is only 6 states in total, whereas you need 8 to label the 8-dim. 3-spin-basis.

It turns out the J^2 spin 1/2 state is doubly degenerate. However, this means you need to invent a new operator to create a new quantum number to resolve this degeneracy.

So, to really recreate the approach for 3-spins you need to provide 8 eigenstates of spin state superpositions (RHS of image) and 8 triples of quantum numbers to label them (LHS of image). You would also need to explicitly write down the 3rd operator in terms of individual spin operators. The result is a complete set of commuting operators J^2, J_z and your new operator.

To test my understanding I've tried this exercise as it requires no more that some linear algebra. I could find a simple operator which can fulfill the role of lifting the degeneracy.
$$\begin{array}{rl}C& =S_1^x{S}_2^y{S}_3^z+S_1^z{S}_2^x{S}_3^y+S_1^y{S}_2^z{S}_3^x\\ & -S_1^x{S}_2^z{S}_3^y-S_1^y{S}_2^x{S}_3^z-S_1^z{S}_2^y{S}_3^x\end{array}$$
It is a simple anti-symmetrisation.
Weirdly, I didn't find this solved anywhere else.