Create accountLogin

Recent searches

No recent searches

Search options

Only available when logged in.
mathstodon.xyz is one of the many independent Mastodon servers you can use to participate in the fediverse.
A Mastodon instance for maths people. We have LaTeX rendering in the web interface!

Administered by:

Server stats:

2.9K
active users

mathstodon.xyz: AboutStatusProfiles directoryPrivacy policy

Mastodon: AboutGet the appKeyboard shortcutsView source codev4.3.7

Public
Dan Piponi

The signed permutation matrices (SPMs) are permutation matrices except that you can use -1 instead of 1. Ie. they are matrices with just one non-zero entry in each row and each column and that entry is 1 or -1.

SPMs form a finite group so their eigenvalues must lie on the unit circle.

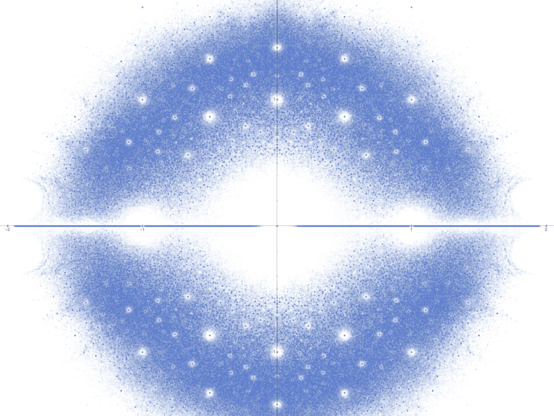
But what about the sum of two SPMs? Here's a plot of the eigenvalues of the sums of 2 8x8 SPMs.

(Sorry, top and bottom cropped, Mathematica has trouble plotting a million points even though seems like a pretty small number to me.)

What can I say? It's kind of like a disc filled with points with lots of smaller circles chopped out and an empty band across the equator and some wispy bits sticking out the sides.
Dan Piponi

A seasonal wreath using the eigenvalues of an SPM + 1/4 another.

Oct 01, 2023, 04:42 PM·Public·Web
2boosts·13favorites
Public
Dan Piponi

Code:

u[d_] := (2 RandomInteger[{0, 1}, d] - 1) IdentityMatrix[d][[
PermutationReplace[Range[d], RandomPermutation[d]]]]

z = Flatten[
Parallelize[
Table[Eigenvalues[u[8] + u[8]/4] // N, {i, 1, 500000}]]];

ListPlot[Transpose[{Re[z], Im[z]}], PlotStyle -> Opacity[0.0025],
AspectRatio -> 1]

SearchLive feeds
About