Recent searches
Search options
The new year is one of my favorite kinds of numbers: a difference of squares!
This observation got me thinking about what kinds of numbers can be written as the difference of squares. For example,
So here’s a little mathematical puzzle to start the new year: Is there a largest number that can not be expressed as the difference of squares? If so, find it. If not, prove no such number exists. Good luck, and happy new year!
https://mrhonner.com/archives/21614
#Math #NumberTheory #2024 #NewYear
@phonner Hi Patrick!
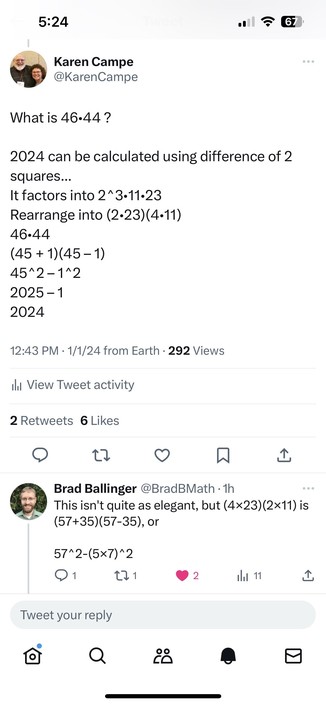
I had noticed the difference of 2 squares opportunity for 2024, and it turns out it can done TWO ways:
45^2 – 1^2
and
57^2 – 35^2
@KarenCampe @phonner There are two more ways to do it.
@davidradcliffe @KarenCampe Figuring out *when* it's possible also allowd you to determine in how many different ways it's possible.
@phonner @davidradcliffe
So I need both factors of 2024 to be even (or both odd, which won't happen with prime factorization 2^3•11•23
Spoiler ahead....