Recent searches
Search options
Finally completed the #Lean4 formalization of my Maclaurin-type inequality paper at https://github.com/teorth/symmetric_project . Specifically, if
is established for
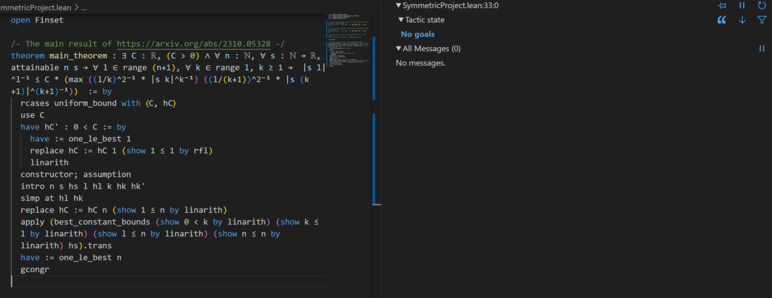
Was surprisingly satisfied to get the blue "No goals" message in the Lean infoview.
In the end it took perhaps a hundred hours of effort, spread out over a month. It was about 20x slower to formalize this paper than it was to write it in LaTeX. Initially this was due to my own inexperience with Lean, though near the end I was hitting the limitations of existing Lean tools, as well as the speed of the Lean compiler (though this was in part due some inefficiencies in my coding). However, Lean is a living language still in development, and several helpful people provided me during this project with upgraded Lean tactics (such as an improved `positivity` tactic that could handle finite sums and products, a `rify` tactic to easily convert natural number inequalities to real number ones, and a `rw_ineq` tactic to implement the rewriting of inequalities I had noted was previously missing). These definitely helped expedite the formalization process, particularly in the last week or so. 1/3
Happily, apart from the one bug previously noted, no other errors (other than very small typos) were detected in the paper. I found some mild simplifications to some steps in the proof as a consequence of formalization, but nothing particularly notable. (But this was a rather elementary paper, and I was not really expecting to glean deep mathematical insights from the formalization process.)
The Sapir-Whorf hypothesis https://en.wikipedia.org/wiki/Linguistic_relativity is controversial for natural languages, but for the specific case of proof formalization languages I think the effect is real. The Lean syntax and library of lemmas and tools certainly pushed me to plan ahead and abstract away many small lemmas to a far greater extent than I would ordinarily do; long "stream of consciousness" type arguments, which I tend to favor personally, are possible in Lean, but often not the most efficient way to proceed. I have also started noticing myself mentally converting results I read in regular mathematical literature to a sort of "Lean pseudocode", though this is probably just a version of the "Tetris effect" https://en.wikipedia.org/wiki/Tetris_effect and will likely dissipate now that my project has concluded.
A combination of automated tools, AI tools, and interactions with human Lean experts proved invaluable. GPT greatly sped up the initial learning of syntax, tools such as `exact?`, `apply?`, and Moogle https://moogle-morphlabs.vercel.app/ helped locate key lemmas, and Copilot had an often uncanny ability to autocomplete one or more lines of code at a time. But there was certainly a lot of "folklore" tips and tricks that I had to go to the Lean Zulip to get answers to. 2/3
@tao Dear Professor Tao, Thank you! Sorry for writing here, but I would like to clarify the steps
"We can thus take expectations and conclude that..."
and "...and hence by (27) we have...", just above Equation (44) in the logarithmically averaged Chowla paper.
Should we sum over
in the representation
where
are the errors?
Is
sufficient?
@consensus This part of the argument does not require the fact that
@tao Thanks! Shouldn't we factor the logarithmic weight
@consensus No. The connection to the original two-point correlation was already worked out in Section 2, where it was calculated that (2.4) implies (2.17). To complete the proof, it suffices to show that (2.17) leads to a contradiction; no further discussion of the original two-point correlation is needed.