Recent searches
Search options
The number pi has an evil twin! It's a number called ϖ with many properties similar to π. There are even mutant trig functions connected to this number, called sl and cl.
So maybe while you were studying trig in high school, some kid in another galaxy was having to memorize all the identities for these other functions.
I doubt it. Just as pi and trig functions are connected to the circle, this number ϖ and its mutant trig functions are connected to a curve shaped like the symbol for infinity, ∞. But this curve is just less important than the circle. I'm not enough of a cultural relativist to believe there's a civilization that cares more about the shape ∞ than the shape ◯.
This ∞-shaped curve is called a 'lemniscate', and ϖ is called the 'lemniscate constant'. I'll show you the lemniscate in my next post.
A civilization will probably only get interested in ϖ when it gets interested in the lemniscate.... or the deeper math it's connected to. On our planet, it was Bernoulli, Euler and Gauss who discovered this math.
(Why does unicode even have the symbol ϖ? Here's why: it's a script version of the Greek letter pi, sometimes called 'varpi' or 'pomega'.)
(1/n)
![The lemniscate constant $\varpi$ is like a mutant version of the number $\pi$:
\[ \pi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^2}} \approx 3.14159 \]
\[ \varpi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^4}} \approx 2.622057 \]
It obeys a lot of similar formulas. For example:
\[ \frac2\pi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12\sqrt{\frac12 + \frac12\sqrt\frac12}} \cdots \]
\[
\frac2\varpi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12 \Bigg/ \!\sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12}} \cdots
\]](https://media.mathstodon.xyz/media_attachments/files/113/703/358/405/037/392/original/12262b712b868b80.jpg "The lemniscate constant $\varpi$ is like a mutant version of the number $\pi$:
\[ \pi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^2}} \approx 3.14159 \]
\[ \varpi = \int_{-1}^1 \frac{dx}{\sqrt{1 - x^4}} \approx 2.622057 \]
It obeys a lot of similar formulas. For example:
\[ \frac2\pi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12\sqrt{\frac12 + \frac12\sqrt\frac12}} \cdots \]
\[
\frac2\varpi = \sqrt\frac12 \cdot \sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12} \cdot \sqrt{\frac12 + \frac12 \Bigg/ \!\sqrt{\frac12 + \frac12 \bigg/ \!\sqrt\frac12}} \cdots
\]")
A culture that may be interested in the mathematics of the shape ∞ are bees!
They often fly in this pattern. (Why?)
@johncarlosbaez Apparently, this is a form of communication.
@MartinEscardo - interesting! I wonder if there is a differential equation that describes a "best" figure-8 curve for an object to fly around in, and whether this curve is the lemniscate. I don't know what "best" means - maybe something about minimizing effort?
Bees do a pretty good job of minimizing wax in their honeycombs.
@johncarlosbaez @MartinEscardo Here's a lemniscate from Euler that arises as a solution to the elastica (the shape a thin elastic rod takes when forced laterally -- these are curves that minimize the bending energy or equivalently the square of the curvature): https://math.stackexchange.com/questions/4509019/the-lemniscate-of-eulers-textitelastica-precise-determination-of-a-charac
see also: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2008/EECS-2008-103.pdf
@NickPizzoOceans - that's very interesting. It seems Euler's lemniscate is different than Bernoulli's has a simple closed form in cartesian and also polar coordinates, while here we see no such thing. However I am not sure they are different, and there some clues hinting that they might be the same - like, both are connected to elliptic functions, and Bernoulli also studied elastica.
@johncarlosbaez @MartinEscardo Bernoulli's seems to be a subset of the Cassini ovals and are defined in terms of a simple algebraic relation. The so-called mechanical aspects of Euler's lemniscate shows the simple ODEs the curve satisfies: https://emis.de/proceedings/Varna/vol9/Djondjorov.pdf
@NickPizzoOceans - I want to know whether Bernoulli's lemniscate is the same as Euler's lemniscate or not!
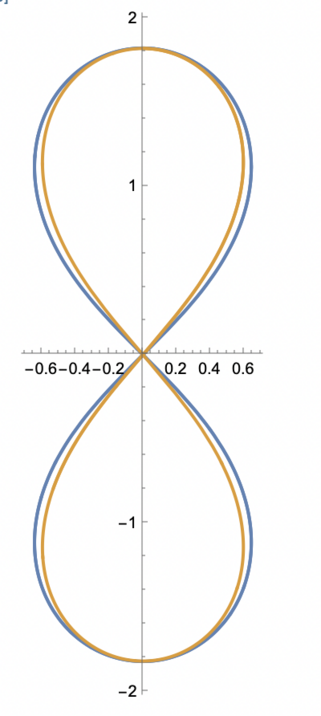
@johncarlosbaez @MartinEscardo They are not. There are a few ways to show this algebraically -- here's an image showing both (Bernoulli in blue, Euler in orange).
Clear["Global`*"]
\[Lambda] = 1; \[Mu] = -0.65223;
k = Sqrt[(1 - \[Mu])/2];
a = Sqrt[(2 (1 - \[Mu])/\[Lambda])];
z[s_] := a*JacobiCN[Sqrt[\[Lambda]]*s, k^2];
x[s_] := 2/Sqrt[\[Lambda]] JacobiEpsilon[s, k^2] - s;
A = 1.82;
ParametricPlot[{{A*Sin[s] Cos[s]/(1 + Sin[s]^2),
A*Cos[s]/(1 + Sin[s]^2)}, {x[s], z[s]}}, {s, 0, 4 \[Pi]}]
